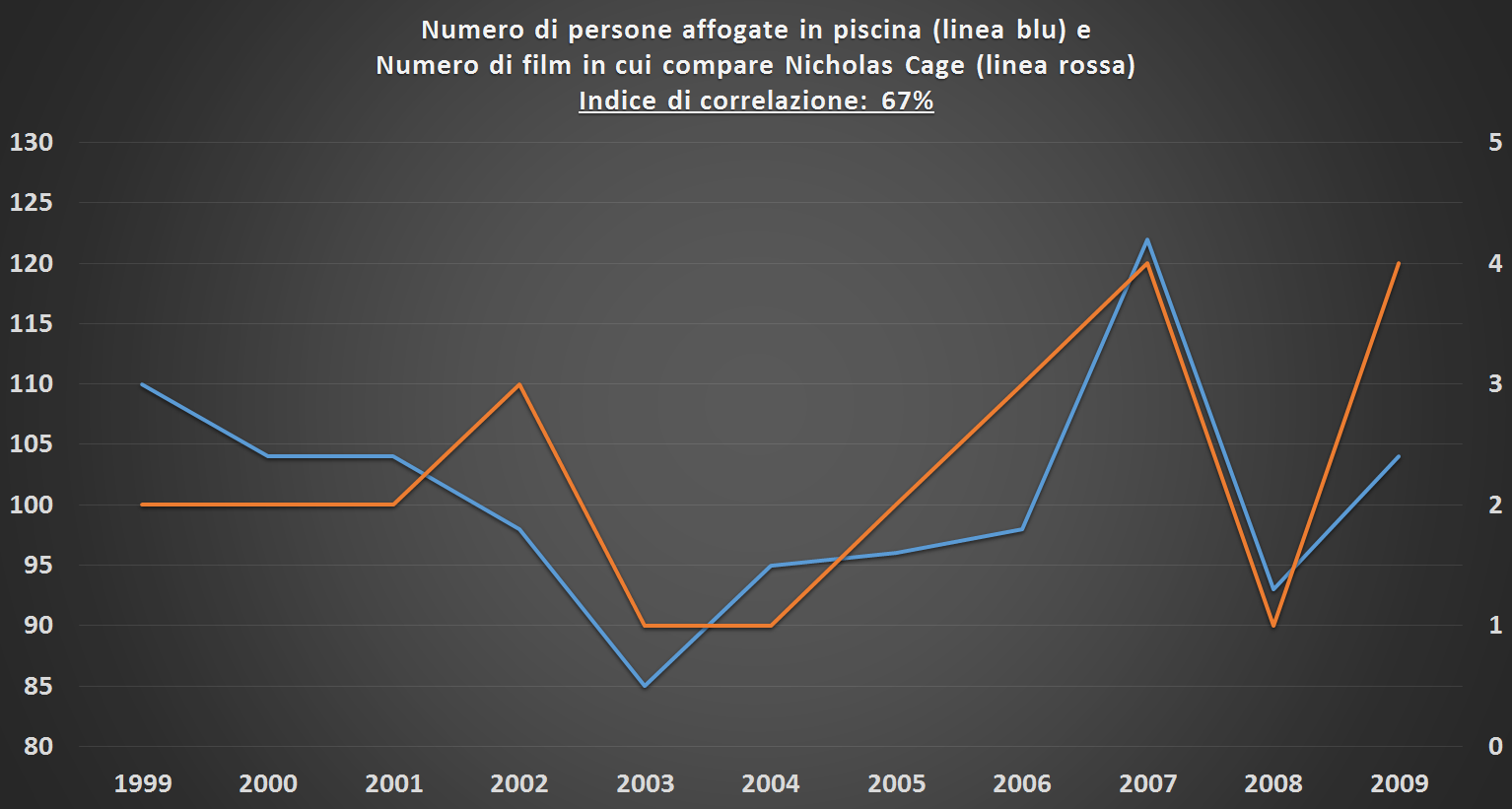
Avete mai sentito dire una frase del genere? “E’ appena uscito un nuovo film di Nicholas Cage, quindi sta per aumentare il numero di persone affogate in piscina”. Probabilmente no, e se davvero l’aveste sentita dire da qualche amico… beh, vi sarete fatti due domande sulla sua sanità mentale. Eppure, guardando il grafico qui sotto – basato su dati reali – il vostro amico sembrerebbe aver ragione.
Cosa ci dice questo grafico? Partiamo da quel numero sottolineato nel titolo, chiamato indice di correlazione. L’indice di correlazione lineare è una misura che descrive quanto varia una misura a seconda del variare di un’altra. Un indice pari al 100% significa che al crescere di una misura, l’altra cresce in modo esattamente proporzionale. Questo indice relativo alle due variabili mostrate nel grafico (numero di persone affogate in piscina e numero di film in cui è presente Nicholas Cage) è pari al 67%, ovvero un valore abbastanza elevato. Questo significa che le due variabili si sono mosse nel corso del tempo quasi a braccetto, e possiamo dunque affermare che esiste una forte correlazione tra le due.
Dove sta allora l’errore? L’errore nell’affermazione iniziale sta nel presupporre un fenomeno di causa-effetto (causalità) tra le due variabili. Il vecchio adagio che qualsiasi studente di statistica ha sicuramente letto almeno una volta nella vita recita infatti “La correlazione non implica causalità”. Oppure, in altri termini, la correlazione è condizione necessaria ma non sufficiente per la causalità.
Sembra un’affermazione banale, ma in realtà non è così scontata come crediamo. Nella frase di cui sopra, è ovvio che solo un folle potrebbe immaginare un nesso di causa-effetto tra le due variabili, ma riportando il concetto a casi più realistici, si può affermare che tutte le misure di correlazione relative a qualsiasi studio statistico non sottendono mai un’ipotesi di causalità. Ogni indice di correlazione produce un risultato meramente numerico, spetta poi a noi stabilire un nesso di causa-effetto basato sulla logicità dei fatti o su determinate ipotesi.
Per quanto incredibile possa sembrare, ci sono molte variabili correlate tra di loro in modo quasi inossidabile (coefficienti di correlazione superiori al 90%), ma che non hanno alcun nesso logico. Ecco alcuni esempi reali relativi agli Stati Uniti negli ultimi anni:
- Consumo pro capite di mozzarella e Dottorati in ingegneria civile (correlazione 95%)
- Consumo pro capite di margarina e Tasso di divorzi nel Maine (correlazione 99%)
- Barili di petrolio greggio importanti in USA dalla Norvegia e Conducenti di auto morti in scontri contro un treno (correlazione 95%)
In tutti questi casi, le due variabili sono così completamente scollegate tra loro che la correlazione elevata è senza dubbio dovuta all’ironia del caso e possiamo escludere con certezza qualsiasi nesso di causa-effetto.
In altri casi, invece, ci troviamo di fronte a situazioni in cui correlazioni apparentemente inspiegabili sono in realtà fenomeni di correlazioni indirette, spesso difficili da interpretare. Pensiamo alle seguenti coppie di variabili
- Consumo di gelato e Numero di attacchi di squali
- Densità di traffico aereo e Spesa per attività culturali
- Numero di bar in città e Numero di bambini iscritti a scuola
Evidentemente non si tratta di correlazioni dirette, dato che in tutti questi casi la prima variabile (A) e la seconda variabile (B) non sono direttamente legate tra di loro. Ma esaminando a fondo, ci accorgiamo che in realtà le due variabili non sono del tutto slegate, bensì sono entrambe legate a una terza variabile latente o non esplicitamente misurata (variabile C), che causa un cosiddetto fenomeno di “correlazione spuria”. Qualche idea? Pensate a queste variabili:
- Temperatura media (entrambi i fenomeni sono più frequenti in estate)
- Reddito pro-capite (entrambi i fenomeni sono più probabili in città con un reddito medio elevato)
- Dimensione della popolazione (entrambi i fenomeni sono legati al numero di persone presenti in città)
Con queste variabili “nascoste” si risolve il mistero delle correlazioni inspiegabili: pur non essendo A e B collegate tra di loro, si ha che la variabile A è collegata a C (variabile latente), e la variabile C è collegata a B.
Ovviamente, a seconda della complessità dello studio, può essere molto difficile capire se un indice di correlazione elevato è dovuto a un fenomeno di causa-effetto, a correlazione spuria o a nessuno dei due casi. Quello su cui va posto l’accento è la necessità di interpretare attentamente ogni indice di correlazione per evitare di trarre conclusione totalmente sbagliate.
Cosa ci resta di questi esempi? Direi una sorta di svilimento della “numerocrazia” intesa come potere dei numeri di spiegare acriticamente la realtà che ci circonda. I numeri e gli indici statistici sono utili, anzi utilissimi, per la comprensione dei fenomeni della realtà, ma necessitano sempre di un’interpretazione e giudizio critico, prima di essere assunti come dogmi ed esprimere un significato probabilmente sbagliato.
Ma per precauzione, la prossima volta che uscirà un film di Nicholas Cage… state lontano dalle piscine! 🙂